I am mostly interested in images and in their mathematical representation and interpretation. My work covers diverse topics such as statistical analysis of visual tasks, segmentation and recognition algorithms, learning, and recently, also 3D point cloud analysis. A selection of my projects over the years is described below. The more recent projects are describe in the Research-recent page (when it is up to date).
Can you believe your algorithms?
Suppose your algorithm suggests some interpretation of a give image. Can we know how reliable these suggestions is ? Knowing that, matters for using the results, and enable online parameter tuning.
The a-contrario methodology enables decision that are based on specific image characteristics. In the colored noise image, for example, lines should not be found, and the threshold selection is challenging.
A. Miaskouvskey, Y. Gousseau, and M. Lindenbaum, Beyond independence: An extension of the a contrario decision procedure, IJCV 101(1), pages 22–44, 2013.

Can we estimate segmentation quality without ground truth?
R. Sandler and M. Lindenbaum, Unsupervised Estimation of Segmentation Quality using Nonnegative Factorization - CVPR08, 2008.
D. Peles and M. Lindenbaum, A segmentation quality measure based on rich descriptors and classification methods, SSVM, 2011.

How many edge points are required to decide that some familiar object is in the scene? The answer quantifies intuitive observations such as "similar objects are harder to discriminate," and depends on object similarity, transformation class, noise, and decision reliability. It allows the ranking of recognition tasks according to their difficulty.
M. Lindenbaum, Bounds on Shape Recognition Performance. IEEE Trans. on PAMI-17, No. 7, pp. 666-680, 1995.
M. Lindenbaum, An Integrated Model for Evaluating the Amount of Data Required for Reliable Recognition, IEEE Trans. on PAMI-19, No. 11, pp. 1251-1264, 1997.
M. Lindenbaum and S. Ben-David, Applying VC-dimension Analysis to Object Recognition. 3rd ECCV, 1994, pp. 239-240

Segmentation and grouping
We considered a common over-segmentation method, which depends on a heuristic parameter and have shown how to estimate this parameter, for the given image, by a known statistical tool. Empirically, the obtained over segmentation achieved the best Recall curve, with some price in boundary roughness.
Local Variation as a Statistical Hypothesis Test, M Baltaxe, P Meer, M Lindenbaum, International Journal of Computer Vision 117 (2), 131-141, 2016.

A generic grouping method, based on maximum likelihood decision
A. Amir and M. Lindenbaum, Quantitative Analysis of Grouping Processes. IEEE Trans. on PAMI-20, No. 2, pp. 168-185, 1998. (A shorter version appeared in ECCV, pp. 371-384, 1996.)
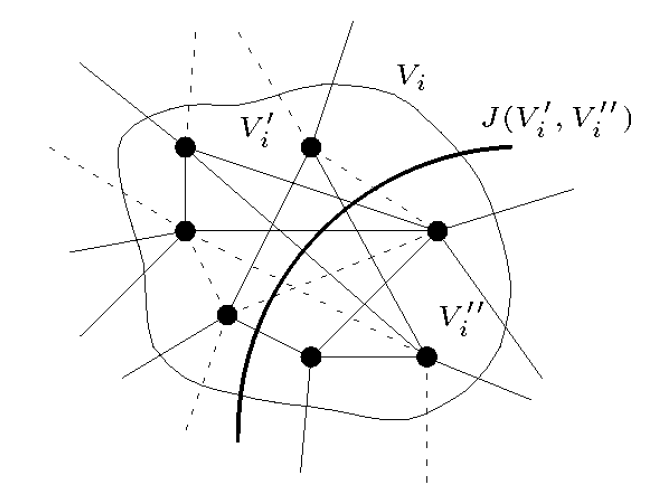
We used statistical model to analysis of the single linkage and the saliency algorithms, revealing the conditions for their success.
A. Berengolts and M. Lindenbaum, On the Performance of Connected Components Grouping. IJCV 41(3), pp. 195-216, 2001.
A. Berengolts and M. Lindenbaum, On the Distribution of Saliency. IEEE Trans. Pattern Analysis and Machine Intelligence, 28(12):1973–1990, 2006. See also ECCV00 and CVPR04 related publications.
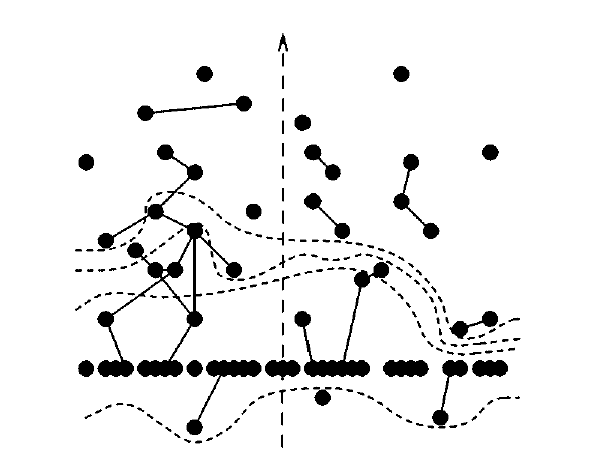
We proposed a method for measuring grouping quality, based on the observation that a better grouping result provides more information about the true, unknown grouping. We show that it is not biased to different types of grouping errors, and it correlates well with human judgment.
E.A. Engbers, M. Lindenbaum and A.W.M. Smeulders, An Information-Based Measure for Grouping Quality. ECCV (3), pp. 392-404, 2004.
Recognition
Comparing images of smooth objects under variable illumination is hard. We modeled the image as correlated Gaussian processes, and used whitening to make an effective comparison. This model also explains why image comparison using Gabor jets is effective as well.
M. Osadchy, D. Jacobs, and M. Lindenbaum Surface Dependent Representations for Illumination Insensitive Image Comparison. IEEE PAMI 29(1):98{111, 2007. See also ECCV04.

Perceptual grouping is informative for object recognition. Intuitively, a good object instance hypothesis should also be a good group. Implementing this condition indeed improves the decision reliability.
A. Amir and M. Lindenbaum, Grouping-based Nonadditive Verification. IEEE Trans. on PAMI-20, No. 2, pp. 186-192, 1998.
Attention
Attention mechanisms specify processing priorities in man and machine vision. Modelling object identities as a set of correlated random variables, led to effective object search and to a characterization of the inherent difficulty of search tasks. Bounds on the possible search performance followed.
T. Avraham and M. Lindenbaum, Attention-based Dynamic Visual Search using Inner-scene Similarity: Algorithms and Bounds. IEEE PAMI 28(2):251-264, 2006. See also ECCV04.
T. Avraham and M. Lindenbaum, Esaliency (Extended Saliency): Meaningful Attention Using Stochastic Image Modeling. IEEE PAMI 32(4), 693-708, 2010.
Psychophysics experiments showed that the search difficulty characterization is valid also for human vision.
Y. Yeshurun, T. Avraham and M. Lindenbaum, Predicting Visual-search Performance by Quantifying Stimuli Similarities. Journal of Vision, 8(4):1{22, 2008.
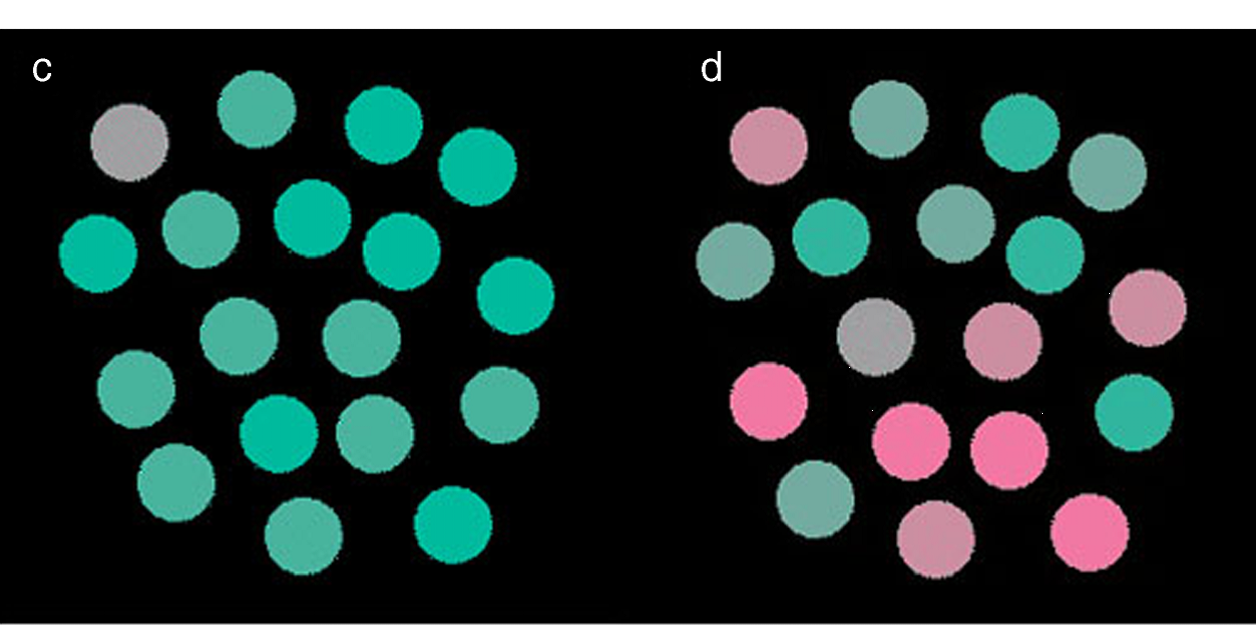
Image processing
The Farthest point sampling (FPS) algorithm
the How to sample an image progressively? We proposed the progressive, Farthest point sampling (FPS) algorithm that places the samples irregularly, and retains deterministic uniformity with the increasing density. By making the uniformity metric image-dependent, the sampling becomes image adaptive.
Yuval Eldar, Michael Lindenbaum, Moshe Porat and Yehoshua Y. Zeevi, The Farthest Point Strategy for Progressive Image Sampling, IEEE Transactions on Image Processing, 6, No. 9, pp. 1305-1315, 1997.

Fast PCA
We proposed two algorithms for accelerate PCA computation. The first uses inner products in the transform domain, while the second works for sequential data (e.g. image stream). This algorithm is faster in typical applications than the usual batch algorithm and allows for dynamic updating.
H. Murase and M. Lindenbaum, Spatial Temporal Adaptive Method for Partial Eigenstructure Decomposition of Large Image Matrices, IEEE Trans. on Image Processing, IP-4, No. 5, pp. 620-629, 1995.
A. Levy and M. Lindenbaum, sequential Karhunen-Loeve Basis Extraction, IEEE Transactions on Image processing 9(8), pp. 1371-1374, 2000. (See also ICIP99.)

NMF with EMD
Non-negative matrix factorization (NMF) isoften more justified when done with the earth movers distance (EMD) rather than the L2 distance. The proposed algorithm indeed achieved better results in applications such as finding texture descriptors from image contacting texture mixtures.
Nonnegative matrix factorization with earth mover's distance metric for image analysis, R Sandler, M Lindenbaum, IEEE Transactions on PAMI 33 (8), 1590-1602, 2011.
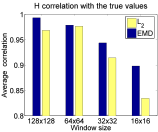
Change detection in high dimensional space
Characterizing distribution in high dimensional space is hard. We characterized distributions using a hierarchical set of minimum volume sets which approximate the levels sets of it density, which led to an effective, generalized, nonparametric, Kolmogorov-Smirnov test for detecting distributional change in high-dimensional data, and to effective hierarchical clustering.
Assaf Glazer, Michael Lindenbaum and Shaul Markovitch, Learning High-Density Regions for a Generalized Kolmogorov-Smirnov Test in High-Dimensional Data. NIPS-2012, 2012.
Assaf Glazer, Michael Lindenbaum, and Shaul Markovitch, q-ocsvm: A q-quantile estimator for high dimensional distributions. NIPS-2013, 2013.
Assaf Glazer, Omer Weissbrod, Michael Lindenbaum, and Shaul Markovitch, Hierarchical mv-sets for hierarchical clustering. NIPS-2014, 2014.
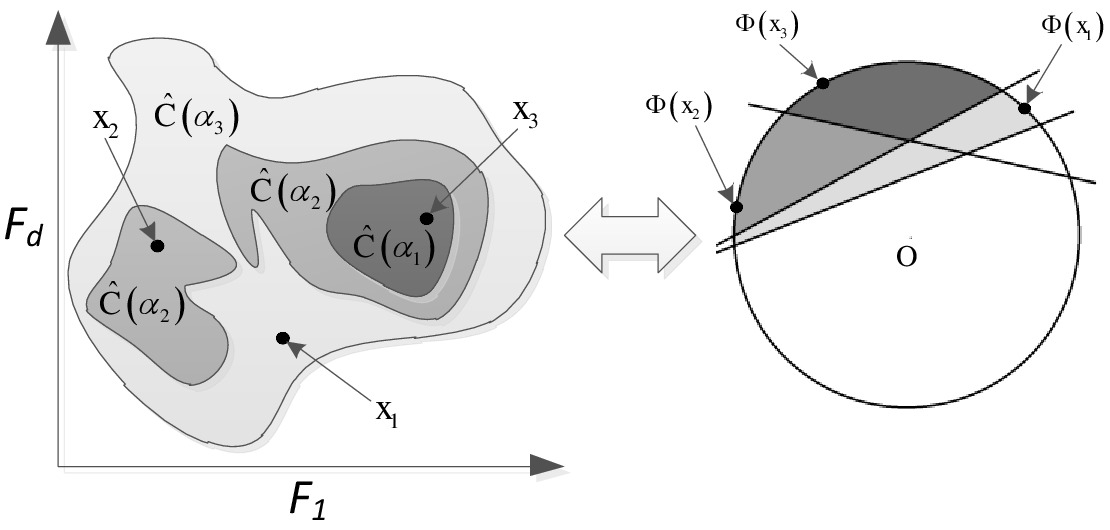
Active learning
We proposed an effective lookahead selective sampling process, based on a random field model.
M. Lindenbaum, S. Markovich, and D. Rusakov, Selective Sampling for Nearest Neighbor Classifiers. Machine Learning 54(2): 125-152 (2004) (Also AAAI99).
VC dimension analysis
Ben-David and M. Lindenbaum, Localization vs. Identification of Semi-Algebraic Sets. Machine Learning 32(3): 207-224 (1998). (Also in COLT93.)
S. Ben-David and M. Lindenbaum, Learning Distributions by their Density Levels - A Paradigm for Learning Without a Teacher. Journal of Computer and Systems Sciences, 1997, pp. 171-182.
Robotics
Geometric probing
My thesis, supervised by Freddy Bruckstein, was concerned with algorithmic robotics. We considered geometric probing tasks, where one is asked to provide a strategy for finding an object's shape using a small number of simple measurements (probes). One part of my thesis was to derive optimal strategies and corresponding lower bounds for parallel probing. The other part was to extend traditional geometric probing, limited to polygonal objects, to smooth object.
M. Lindenbaum and A. Bruckstein, Parallel Strategies for Geometric Probing . Journal of Algorithms 13, pp. 320-349, 1992.
M. Lindenbaum and A. Bruckstein, Blind Approximation of Planar Convex Shapes, IEEE Trans. on Robotics and Automation, RA-10, No. 4, pp. 517-529, 1994.
Distributed Ant Robotics
Inspired by ant communication we considered a group of robots, which communicate only by leaving traces, to cover an unmapped region (for, e.g., cleaning). We developed discrete (graph based) and continuous strategies that are able to guarantee coverage even if some of the robots stop functioning and when the region changes it connectivity. One example is:
Distributed covering by ant-robots using evaporating traces, IA Wagner, M Lindenbaum, AM Bruckstein, IEEE Transactions on Robotics and Automation 15 (5), 918-933, 1999.

